佐藤 弘康 准教授
Laboratory
アダマール多様体とよばれる曲率が零以下の空間の幾何学と、確率密度関数の空間上の幾何学(=情報幾何学)の研究をしています。アダマール多様体は数空間 $\mathbb{R}^n$ と同相であり、 「どこまでも歩いていける」空間ですが、 理想境界とよばれるコンパクトな空間が縁を囲んでいます。この理想境界上の情報幾何を用いて、 アダマール多様体の性質を明らかにできないか調べています。
小学校で「三角形の内角の和は180°である」ことを習いますが、それは曲がっていない平らな空間における性質であり、一般には正しくありません。例えば、地球のような丸い球面上で三角形を描けば、その内角の和は180°を超えてしまいます。円板(周を含まない円の内部)に対し、「周に直交する円弧」を「まっすぐな線」と定めると、三角形の内角の和は180°より小さくなります。三角形の内角の和が180°より大きいか小さいかとう性質は、空間の曲がり方を表す「曲率」という概念として一般化されます(図1参照)。
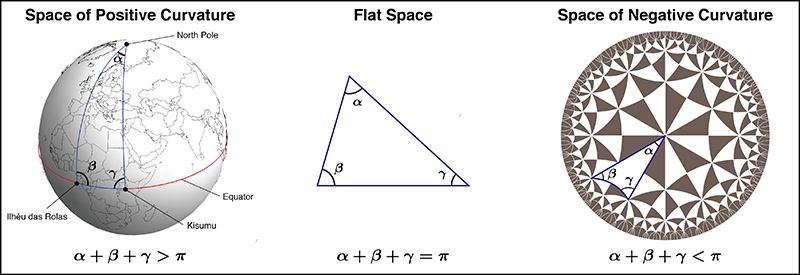
図1
このような曲がった空間をリーマン多様体といい、その上の幾何学のことをリーマン幾何学といいます。リーマン多様体は、いわば仮想的に実現された空間ですが、相対性理論はリーマン幾何学が土台となり構築されました。 アダマール多様体とは、曲率が至る所0以下で、完備,単連結なリーマン多様体のことです。このような空間上の調和性、漸近的調和性、可視性などの性質の関係と、Damek-Ricci空間とよばれる特別なアダマール多様体の性質について研究しています。
現代幾何学の主な対象である多様体とは、各点の近傍に必ず座標がはいる集合、つまり、点の位置を数の組として表せるような集合のことです。地球(=球面)上の位置は緯度と経度という2つの数の組で表せるので、球面は2次元多様体となります。逆に、座標が定義できる集合は多様体の構造をもち、幾何学の対象となります。例えば、確率論や統計学でとても重要な確率分布である「正規分布」は平均 $\mu$ と分散 $\sigma^2$ を与えると密度関数が決まるので、 $(\mu, \sigma)$ が座標となり、 正規分布全体の集合は多様体の構造をもちます。さらに, ある統計量に由来する幾何構造を与えることにより正規分布の全体は負の定曲率をもつ2次元双曲空間となります(図2参照)。
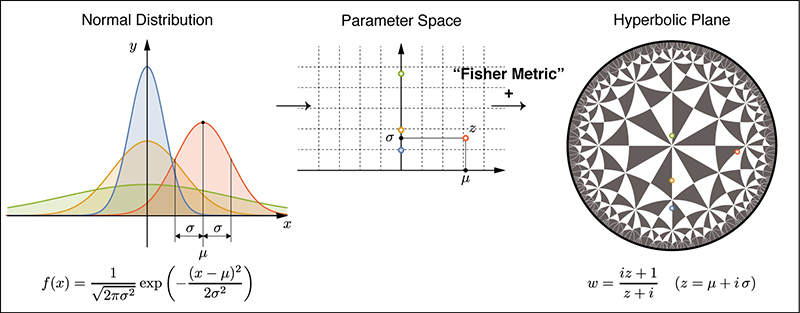
図2
このように確率分布の集合を多様体とみて、その上の幾何構造を研究する分野を情報幾何学といい、統計学や情報科学に応用されています。私は確率分布の全体からなる無限次元の空間上の情報幾何に興味を持っています。Damek-Ricci空間とよばれる特別なアダマール多様体は,理想境界上の情報幾何の観点でみると。ある良い性質をもつ空間と特徴づけることができます。情報幾何学的なアプローチでアダマール多様体の性質を明らかにできないか、研究しています。
数学を深く学びたい学生へ
工学に応用される数学を深く学びたい、数学の教職免許をとりたい、数学科の大学院に進学したい…そんな学生さん、数学の本を読んでセミナーしませんか。数学の本をどう読み、どう理解すればいいか、週一回程度、セミナー形式で指導します。数学の知識や数学的な考え方が身につくだけでなく、どう説明すれば相手に理解してもらえるか、プレゼンテーションの基礎の訓練にもなります。数学に興味がある学生はぜひ私の研究室を訪ねてみてください。

セミナー風景