衛藤 和文 教授
Laboratory
数学を研究しています。数学の中でも代数学を中心に研究を行っています。また、工学の諸問題の数学モデル化にも興味を持っています。例えば、材料の表面にやすりがけを行うのにどのようにやすりを動かすと表面を均一に削ることができるか、またどのようにやすりを制御すべきかの問題は、実際に実験してみてよい方法は見つかるかもしれませんが、それがベストだとは言い切れないでしょう。そこを理論付けるのが数学だと思います。このように、役に立つことが実感できる数学の研究を目指していけたらいいなと思いながら日々過ごしています。

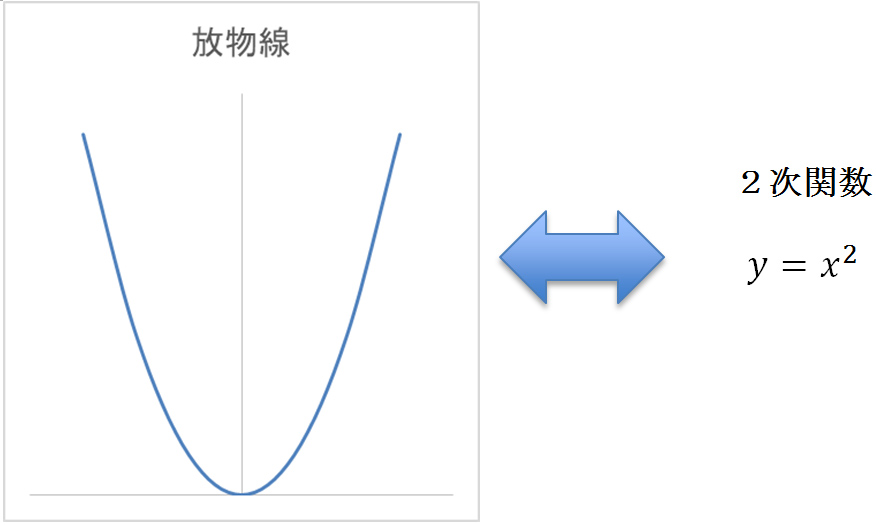
高校までに、2次関数と放物線の関係を学んだと思います。つまり、式と図形の間に対応があるのです。そこで、図形の性質を調べるのに、どのような式で表されているかは重要で、それを具体的に与えることを研究しています。ここで考えている図形は、平面や空間内の図形だけではなく、4次元以上の空間にある図形も考えています。この場合、式は1つだけとは限りません。例えば、空間内の直線の方程式を表すには2つの式が(等号が2つ)必要です。ですので、いくつ式があればよいかは非常に重要な問題の1つです。細かい言葉の定義は省きますが、次の19世紀の有名な数学者であるクロネッカーの論文に由来する予想はまだ解けていません。
$n$ 次元アフィン空間内の代数曲線は $n-1$ 個の式で表すことができる。
代数曲線とは、空間内の曲線を思い浮かべてもらうとよいと思います。それは、2つの曲面の交わりとして表されるということを主張しています。
ここからは少し専門的な話をしていきたいと思います。アフィン空間内の代数曲線でない場合、すでに上の予想が成り立たないことが知られています。したがって、アフィン空間内で考えることが重要です。また、代数曲線の中でも最も単純な曲線であるモノミアル曲線を研究対象としています。モノミアル曲線とは、パラメータが1つ与えられ、各座標がそのパラメータのべきで表されるような曲線を指します。このような場合ですら、完全にはわからないのです。
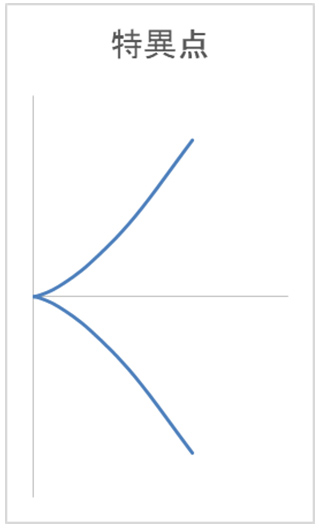
また、なぜこのような曲線を考えるのかには、別の理由もあります。モノミアル曲線の原点は様々な特異点を与えてくれるのです。特異点を代数的に研究する分野を代数幾何学といい、その中で式を重視しながら研究していく分野を可換環論といいます。可換環論において、どのくらい特異点の種類があるのかというのは重要な研究テーマです。逆に、特異点を分類するために、どのような性質に注目すればよいかを探すことも重要です。モノミアル曲線の原点を特異点の代表例として調べる、またそのためにどのような方程式で表すことができるかを知ることは基本的で、大事な内容になります。ですので、モノミアル曲線を対象とした、必要な方程式の個数に関する研究を続けているのです。
皆さんは、大学の先生は、大学で授業を行っているので、大学教育に関しての専門家であると思っているかもしれません。もちろん、よりよい授業を行うために、どの先生も日々努力しています。しかし、大学で数学の授業を行うにあたってはそれだけでは不十分です。まず、皆さんが中学校、高校等でどのような授業を受けてきたのかを知っておかなければなりません。もちろん、授業内容もそうですが、勉強の仕方についても知り、研究する必要があります。次に、どのような内容を大学で教えるべきか、また新たな教育内容を考えるにあたり必要な歴史的観点からの教育内容の変遷の研究も行っています。最後に、このような研究を行った成果として、いくつか教科書を作成しました。下の写真がそうです。
